This is one of the basic interview question about algorithm about finding the two numbers from array such that there sum is equal to K.
In this post, we'll look into different approaches for finding all the pair of integer such that there sum is equal to K.
Approach 1 Brute-Force
In this approach, for each input element check whether there is any element exist whose sum is K. This can be solved with just two loops.
Time Complexity : O(n^2) for nested loops, Space Complexity : O(1)
Approach 2
In this approach, we first sort the array using merge or heap sort which give O(nlogn) complexity. Then on sorted array we main two indices, i point to starting index and j point to last element index. We compute A[i]+A[j]. If sum equals K, then we found the pair increment both i & j. If the sum is less then k, increment i, if sum is greater than K decrements j.
Time Complexity : O(nlogn) if array is already sorted then complexity would be O(n), Space Complexity : O(1)
Approach 3
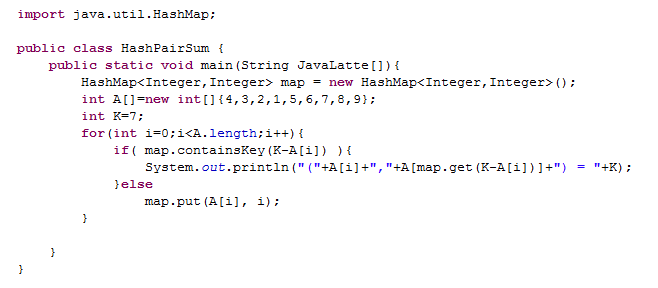
In this approach we use HashMap, our task is find two indexes of the array whose sum is K i.e, A[i]+A[j]=K. For each input element A[i] we check whether K-A[i] also exist in the Hash map. key will be array element, value will be index of element.
Time Complexity : O(n) , Space Complexity : O(n)
If you know anyone who has started learning Java, why not help them out! Just share this post with them.
Thanks for studying today!...
In this post, we'll look into different approaches for finding all the pair of integer such that there sum is equal to K.
Approach 1 Brute-Force
In this approach, for each input element check whether there is any element exist whose sum is K. This can be solved with just two loops.
Time Complexity : O(n^2) for nested loops, Space Complexity : O(1)
Approach 2
In this approach, we first sort the array using merge or heap sort which give O(nlogn) complexity. Then on sorted array we main two indices, i point to starting index and j point to last element index. We compute A[i]+A[j]. If sum equals K, then we found the pair increment both i & j. If the sum is less then k, increment i, if sum is greater than K decrements j.
Time Complexity : O(nlogn) if array is already sorted then complexity would be O(n), Space Complexity : O(1)
Approach 3
In this approach we use HashMap, our task is find two indexes of the array whose sum is K i.e, A[i]+A[j]=K. For each input element A[i] we check whether K-A[i] also exist in the Hash map. key will be array element, value will be index of element.
Time Complexity : O(n) , Space Complexity : O(n)
If you know anyone who has started learning Java, why not help them out! Just share this post with them.
Thanks for studying today!...




Second approach is very effective approach.
ReplyDeleteBut i have doubt in third solution, suppose if there are duplicate elements in array how will you be finding the pair.
Suppose 4 is duplicate in array, and you have to find pairs whose sum is 8.
Or there is only one 4 and you have to find pairs whose sum is 8.
I think for above two scenario it will contradict. Let me know if I am wrong.
I didn't get your two scenario. Please given an array where you think this will contradict.
DeleteSuppose the array is - {4,5,9,7,3,1,2,0,6,4,5}, and the value of k is 8.
Deletenow you insert all these elements in hashmap and you will pick element 4 and check if (8-4) is available in map, will return true and {4,4} will be a pair, which is correct since there are two 4's in array.
Now assume the array is - {4,5,9,7,3,1,2,0,6,5}, and the value of k is 8.
now you insert all these elements in hashmap and you will pick first element 4 and check if (8-4) is available in map, it will return true but {4,4} will not be a pair now, because there is only one 4 in the array.
I think you misunderstood the code. Please read it once again.
Deleteif(map.containsKey(k-a[i])){
System.out.println(a[i]+" "+a[map.get(k-a[i])]+" "+k);
}else
map.put(a[i],i);
}
In this condition, first I check whether the element is in the hashmap or not. If not, then I insert the element otherwise we get the pair. Why don't you try the code?